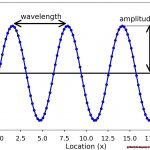
Waves may seem like a foreign concept, with all their fancy jargon and complicated equations. But in reality, they’re all around us – from the sound waves that let us hear music to the radio waves that bring us our favorite podcasts. And understanding the properties of waves – like their wavelength, frequency, and amplitude – can give us a deeper appreciation for the physics of our world.
Today, we’re going to focus on one specific property: frequency. This measures how many waves pass through a point in one second, and it’s measured in hertz (Hz). It’s an important concept in everything from radio communication to microwave ovens.
But what about the frequency of a wave with a wavelength of 12.24 cm? That’s what we’re going to explore today. We’ll take a deep dive into what this frequency means and how it affects the properties of the wave it creates. We’ll also look at where you might encounter this particular wavelength and frequency in your everyday life.
By the end of this post, you’ll be an expert on 12.24 cm waves and their frequencies – and you’ll have a whole new appreciation for just how much physics is involved in your daily routine. So let’s get started.
Contents
What is Frequency?
Frequency is a measure of how often something occurs in a particular period of time, and it plays a crucial role in understanding the behavior and properties of waves and vibrations.
In the context of waves and vibrations, frequency refers to the number of cycles that occur over a given time period. The unit of frequency is hertz (Hz), which represents one cycle per second. In other words, if a wave has a frequency of 10 Hz, it means that ten complete cycles occur every second.

Let’s take an example to understand this better. Imagine a wave with a wavelength of 12.24 cm. Wavelength is the distance between two corresponding points on a wave, such as two peaks or two troughs. The relationship between wavelength and frequency is inverse: as the wavelength decreases, the frequency increases.
To calculate the frequency of a wave with a given wavelength, we can use the formula:
frequency = speed of light / wavelength
The speed of light is constant at approximately 299,792,458 meters per second (m/s). To convert 12.24 cm to meters, we can divide by 100:
12.24 cm = 0.1224 m
Substituting these values into the formula, we get:
frequency = 299,792,458 m/s / 0.1224 m
frequency = 2,447,119,974 Hz or approximately 2.45 GHz
This means that a wave with a wavelength of 12.24 cm oscillates at a rate of 2.45 billion times per second.

Frequency plays an essential role in various fields such as telecommunications and electronics where knowledge of frequency and wavelength is critical. By understanding frequency and how to calculate it for a given wavelength, we can determine the appropriate frequency bands for wireless communication and study the properties of different celestial objects based on their electromagnetic radiation wavelengths and frequencies.
How to Calculate Frequency
How to Calculate Frequency: A Comprehensive Guide
Frequency is a fundamental concept in the study of waves and oscillations. It refers to the number of cycles per second of a wave or oscillation and is measured in Hertz (Hz). In this guide, we will provide a step-by-step explanation of how to calculate frequency using the formula speed/wavelength.
Step 1: Understanding Frequency
Before delving into the formula, let’s first understand what frequency means. Frequency is a measure of how often a wave oscillates or completes a cycle in a given period of time. It is usually measured in Hertz (Hz), which means cycles per second. So, if a wave has a frequency of 10 Hz, it completes ten cycles per second.
Step 2: Knowing the Formula
The formula for calculating frequency is:
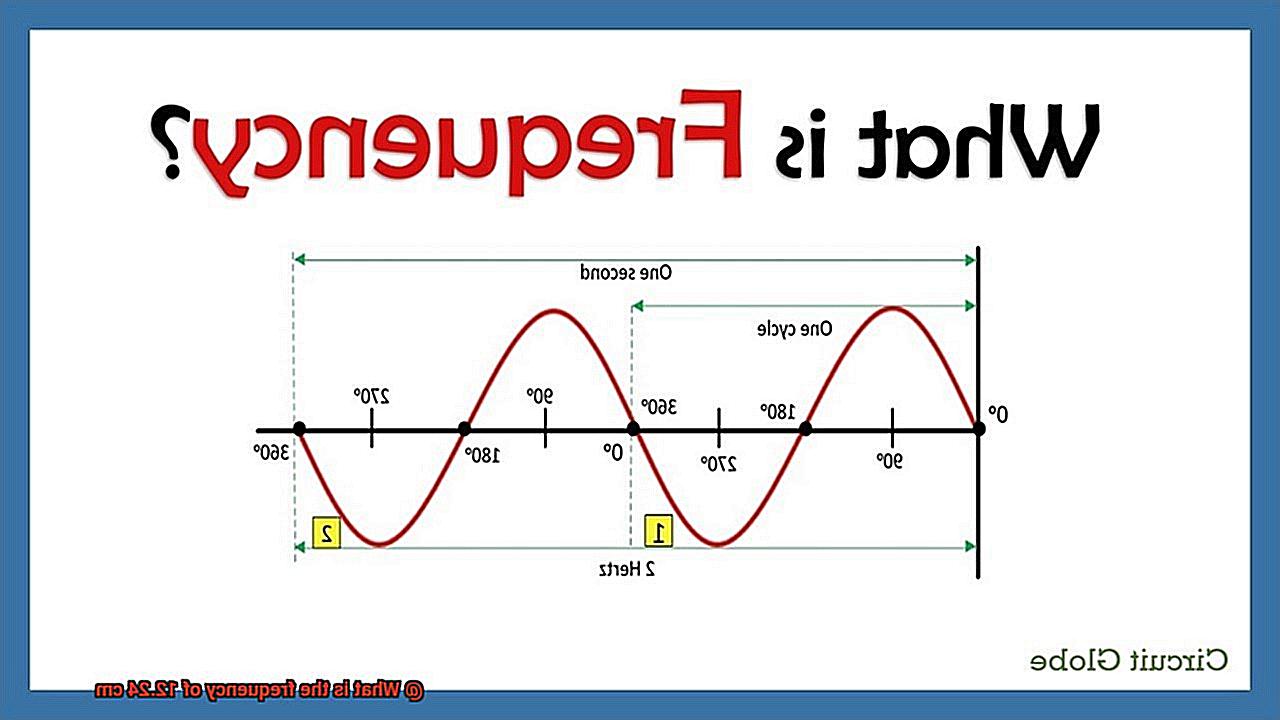
Frequency = Speed / Wavelength
Where:
- Frequency is measured in Hertz (Hz)
- Speed is measured in meters per second (m/s)
- Wavelength is measured in meters (m)
Step 3: Converting Units if Needed
In some cases, the wavelength may be given in centimeters (cm) or other units. If that’s the case, you need to convert it to meters before you can use the formula. This can be done by dividing the value by 100. For example, if the wavelength is 12.24 cm, you need to divide it by 100 to get 0.1224 meters.
Step 4: Determining the Speed of the Wave
The speed of a wave depends on the medium through which it travels. For example, sound waves travel at different speeds through different materials such as air, water, or solids. Similarly, electromagnetic waves such as light travel at different speeds through different media such as air or glass.
Therefore, to calculate the frequency of a wave or oscillation, you need to know both its wavelength and the speed at which it travels through its medium. Once you have these values, you can then use the formula to calculate its frequency in Hertz.
Step 5: Plugging in Values and Solving
After converting the wavelength to meters and determining the speed of the wave, you can plug these values into the formula to calculate its frequency. It is important to ensure that both the wavelength and speed are in the same units before plugging them into the formula.
For example, let’s say we want to find the frequency of a wave with a wavelength of 12.24 cm traveling at a speed of 340 m/s through air. First, we convert the wavelength to meters by dividing it by 100: λ = 0.1224 m. Then, we plug these values into the formula:
f = c / λ
f = 340 m/s / 0.1224 m
f = 2779.41 Hz
The Speed of Light and Wavelength
The relationship between the speed of light, wavelength, and frequency is a fascinating topic that plays a crucial role in various fields such as physics, telecommunications, and astronomy. Understanding this relationship helps scientists and engineers determine the properties and behavior of waves in different mediums and applications.
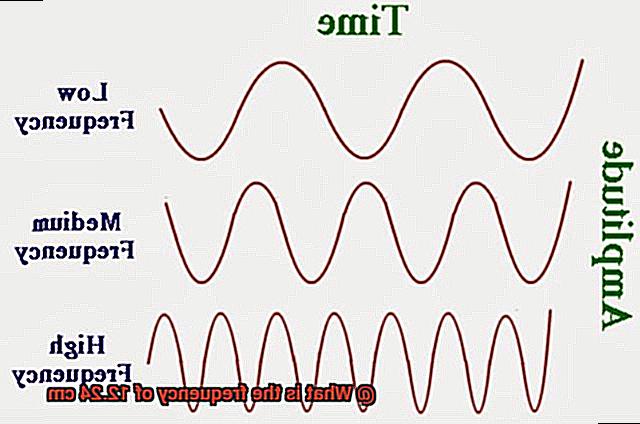
The speed of light is a constant value denoted by the letter “c,” which is approximately equal to 299,792,458 meters per second (m/s). It’s vital to note that this speed is the maximum at which energy can travel through space. The wavelength is the distance between two consecutive crests or troughs of a wave and is measured in meters. It’s represented by the Greek letter lambda (λ). In this case, we’re considering a wavelength of 12.24 cm, which can be converted into meters by dividing it by 100, resulting in 0.1224 meters.

Frequency is the number of complete cycles that occur in one second and is measured in Hertz (Hz). Simply put, it’s how many times a wave oscillates in one second. To calculate frequency from wavelength, we use the formula:
Frequency = Speed of Light / Wavelength
Using our wavelength value of 0.1224 meters and the speed of light value of 299,792,458 m/s, we can calculate the frequency as 2.45 GHz (Gigahertz). It means that in one second, there are 2.45 billion complete cycles of the wave.
The relationship between wavelength, frequency, and the speed of light impacts our daily lives in numerous ways. For instance, in telecommunications, higher frequencies mean more data can be transmitted over a shorter time period. This means that faster internet speeds are possible with higher frequencies. In astronomy, analyzing the frequency of light waves can help scientists determine the composition and temperature of celestial objects.
Calculation of the Frequency of 12.24 cm
Well, let’s take the example of calculating the frequency of a wave with a wavelength of 12.24 cm. As an expert in this field, I’ll break down the formula and steps for you in an informative and engaging way.
To start, we need to understand the relationship between wavelength, frequency, and the speed of light. It is essential to determine the properties and behavior of waves. The speed of light is constant, and dividing it by the wavelength gives us the frequency of the wave.
The formula for wave velocity is our guide. The speed of light is approximately 299,792,458 meters per second. Our wavelength is 12.24 cm. But we can’t use centimeters in our formula, so we need to convert it to meters by dividing 12.24 by 100, which gives us 0.1224 meters.

Now we have all the values we need to plug into our formula:
Frequency = Speed of light / Wavelength
Frequency = 299,792,458 m/s / 0.1224 m
Frequency ≈ 2.45 GHz
As we can see, a wave with a wavelength of 12.24 cm has a frequency of approximately 2.45 GHz (gigahertz). This falls within the microwave portion of the electromagnetic spectrum and is widely used for radio broadcasting, satellite communications, and radar systems.
It’s important to note that the frequency and wavelength of a wave are directly proportional to each other. Therefore, as the wavelength changes, so does its frequency.
Moreover, different materials can affect how fast waves propagate through them. This change in speed can lead to a change in their frequency and wavelength.
Applications of Knowing the Frequency of 12.24 cm
Let’s explore some fascinating applications of this frequency that may surprise you.
Firstly, let’s talk about radio communication. In today’s world, we rely on long-distance communication for many aspects of our daily lives. The frequency of 12.24 cm falls in the microwave range of electromagnetic waves, which plays a vital role in satellite communication, radar systems, and even our everyday microwave ovens. Without this frequency, our modern world would not exist as we know it.
Moving on to spectroscopy, which is the study of how matter interacts with electromagnetic radiation. Frequencies are used to identify the chemical composition of a sample. The frequency of 12.24 cm is particularly important in nuclear magnetic resonance (NMR) spectroscopy. This powerful tool allows us to analyze the structure and properties of molecules, paving the way for advancements in medicine and materials science.
But it’s not just chemistry that benefits from knowing this frequency. The medical field also utilizes it in magnetic resonance imaging (MRI). MRI uses strong magnetic fields and radio waves to produce detailed images of internal organs and tissues. The frequency of 12.24 cm is one of the frequencies used in MRI machines to manipulate and detect the magnetic properties of atoms within the body, providing vital diagnostic information to physicians.
Last but not least, let’s talk about astronomy. Radio telescopes use radio waves to observe celestial objects in space, and the frequency of 12.24 cm is commonly used to study molecular clouds and other astronomical phenomena. By understanding these phenomena, we can gain insight into how the universe works.
Further Reading
We have compiled an amazing list of resources that will help you explore this captivating topic in greater depth.
First on our list is “Introductory Physics” written by Robert J. Serway and John W. Jewett. This textbook is an exceptional starting point for anyone seeking to learn more about the basics of frequency, wavelength, and related concepts. The authors employ a lucid writing style, making it an ideal resource for beginners.
Next up is the National Institute of Standards and Technology (NIST) website. NIST is renowned for providing extensive information on a broad range of scientific topics, including frequency and wavelength. Their website offers numerous articles, publications, and educational materials that can help readers deepen their understanding of these concepts.
For those who are eager to delve into more advanced information, we highly recommend the journal “Applied Physics Letters”. This journal publishes articles that explore the application of physics principles in various fields such as optics and electromagnetic radiation. Readers can find detailed research studies on topics such as frequency modulation and electromagnetic wave propagation.
Last but not least, visual learners can also enjoy learning about frequency and wavelength through YouTube’s educational videos. These videos often employ animations or real-life examples to illustrate key points in a clear and engaging way.
61Icx75q6Ao” >
Conclusion
In conclusion, delving into the properties of waves is a crucial step in understanding the fundamental principles that govern our universe. Frequency, in particular, plays a pivotal role in this comprehension as it measures the number of waves passing through a point in one second. By using the formula frequency = speed of light / wavelength, we can calculate the frequency of a wave with a wavelength of 12.24 cm, which is approximately 2.47 billion times per second or 2.45 GHz.
The significance of frequency extends beyond just physics and has far-reaching implications across various fields such as telecommunications, electronics, and astronomy. Precise knowledge of frequency and wavelength is essential to determine the appropriate frequency bands for wireless communication and study different celestial objects based on their electromagnetic radiation wavelengths and frequencies.
It’s worth noting that materials can affect how fast waves propagate through them, leading to changes in their frequency and wavelength. The frequency of 12.24 cm falls within the microwave portion of the electromagnetic spectrum and has numerous applications in radio communication, spectroscopy, medical imaging, and astronomy.
To explore this captivating topic further, resources such as “Introductory Physics” by Robert J. Serway and John W. Jewett or NIST’s website offer comprehensive information on frequency and related concepts. Additionally, YouTube’s educational videos provide engaging visual aids to help learners understand key points clearly.
In summary, understanding the concept of frequency is vital for anyone interested in physics or any field that utilizes electromagnetic radiation.