Have you ever stopped to think about the invisible waves that surround us every day? From the radio stations we listen to on our commute to the Wi-Fi signals that power our digital lives, electromagnetic waves are everywhere. But what about the 12cm wavelength? This particular wavelength has been making a splash in the world of communication, and for good reason.
So, what exactly is the frequency of 12cm wavelength and why is it so important? To understand this, we first need to get back to basics. Wavelength refers to the distance between two adjacent peaks or troughs of a wave. In other words, it’s how long one complete cycle of the wave is. Frequency, on the other hand, refers to how many cycles pass by a point in one second. So when we talk about the frequency of 12cm wavelength, we’re referring to how many times per second those peaks and troughs occur.
But why does this matter? Well, as it turns out, the frequency of 12cm wavelength has some pretty significant applications in our daily lives. From microwave ovens that use these waves to cook our food quickly and efficiently to communication towers that rely on them for transmitting data over long distances, understanding this frequency can help us better understand how these technologies work.

So join me as we explore all things electromagnetic spectrum and radio waves and dive into the fascinating world of 12cm wavelength frequency. It’s sure to be an illuminating journey.
Contents
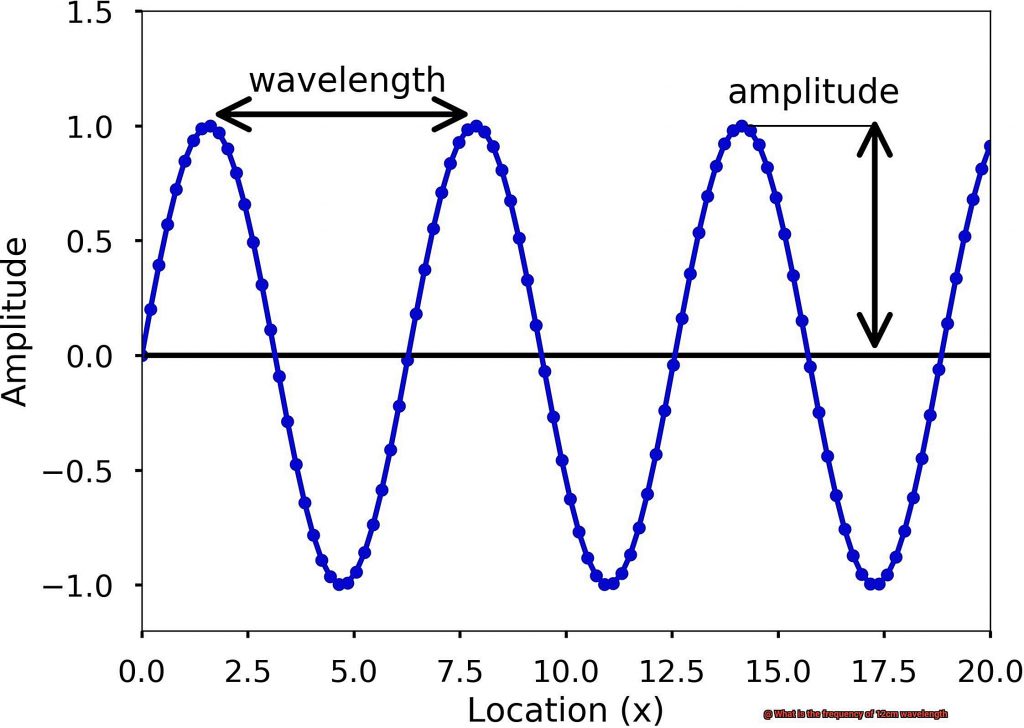
What is Wavelength?
The answer lies in the fundamental concept of wavelength. Wavelength refers to the distance between two consecutive points on a wave that are in phase with each other. In simpler terms, it is the distance between two consecutive peaks or troughs of a wave.
Wavelength is measured in units of distance, such as meters, centimeters, or nanometers. This measurement determines the properties of waves, including their frequency and energy. Waves with shorter wavelengths have higher frequencies and more energy, while waves with longer wavelengths have lower frequencies and less energy.
Wavelength and frequency are two sides of the same coin. Frequency refers to the number of waves that pass through a given point in one second. For electromagnetic waves, such as light and radio waves, the speed of the wave is constant at approximately 3 x 10^8 meters per second. Therefore, we can use the formula c=λν (where c is the speed of light, λ is the wavelength, and ν is the frequency) to calculate the frequency of a given wavelength.
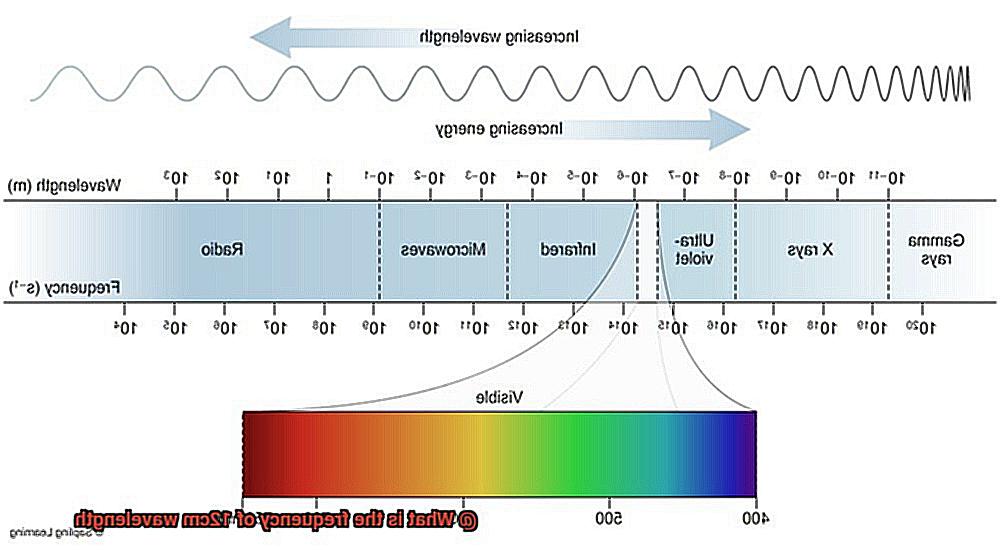
Now let’s take a closer look at light waves. The wavelength of a light wave determines its color. Red light has a longer wavelength than blue light. This is why we see different colors in a rainbow, as each color corresponds to a different wavelength of light.
But the importance of wavelength doesn’t stop there. It can also be applied to mechanical waves, such as sound waves. In fact, our ability to hear different pitches is due to differences in wavelength.
Finally, let’s explore some practical applications of wavelengths. Remember that microwave oven we mentioned earlier? It uses microwaves with a frequency of approximately 2.5 billion Hertz (Hz), which falls within the microwave region of the electromagnetic spectrum. Additionally, radar technology also utilizes microwaves for detection purposes.
What is Frequency?
The answer lies in the fundamental concept of frequency.
Frequency is a measurement of the number of cycles of a wave that occur per second. It is denoted by the symbol ‘f’ and measured in hertz (Hz). Wavelength, on the other hand, is the distance between two consecutive peaks or troughs of a wave and is usually denoted by the Greek letter lambda (λ) and measured in meters.
The relationship between frequency and wavelength is inverse – as the frequency increases, the wavelength decreases, and vice versa. This relationship is governed by the wave equation, which states that the product of frequency and wavelength equals the speed of light in a vacuum (c).
To put this into perspective, imagine standing at the beach, watching waves roll in. The distance between each wave’s crest or trough is its wavelength, while the number of waves that pass by per second is its frequency. By understanding this relationship, we can appreciate how different frequencies relate to different wavelengths and understand why they are important.
Understanding frequency is crucial in many areas of science and engineering. Telecommunications systems rely on specific frequencies to transmit signals over long distances without interference. Radio astronomers use frequencies to study celestial objects and understand the universe’s structure and evolution. Medical imaging techniques such as MRI also use specific frequencies to create detailed images of internal organs and tissues.
By knowing the frequency of a wave, we can determine its properties such as energy, amplitude, and phase. This information allows us to design and optimize systems that transmit or receive signals at specific frequencies.
The Connection Between Wavelength and Frequency
The relationship between wavelength and frequency is a fundamental concept in this field. Electromagnetic waves are oscillating electric and magnetic fields that propagate through space at the speed of light. These waves have different frequencies and wavelengths, which determine their properties and how they interact with matter.
Wavelength is the distance between two consecutive peaks or troughs of a wave, denoted by the Greek letter lambda (λ), and measured in meters, centimeters, or nanometers. Frequency, on the other hand, is the number of oscillations or cycles per second of a wave, symbolized as f or nu (ν), and measured in hertz (Hz).
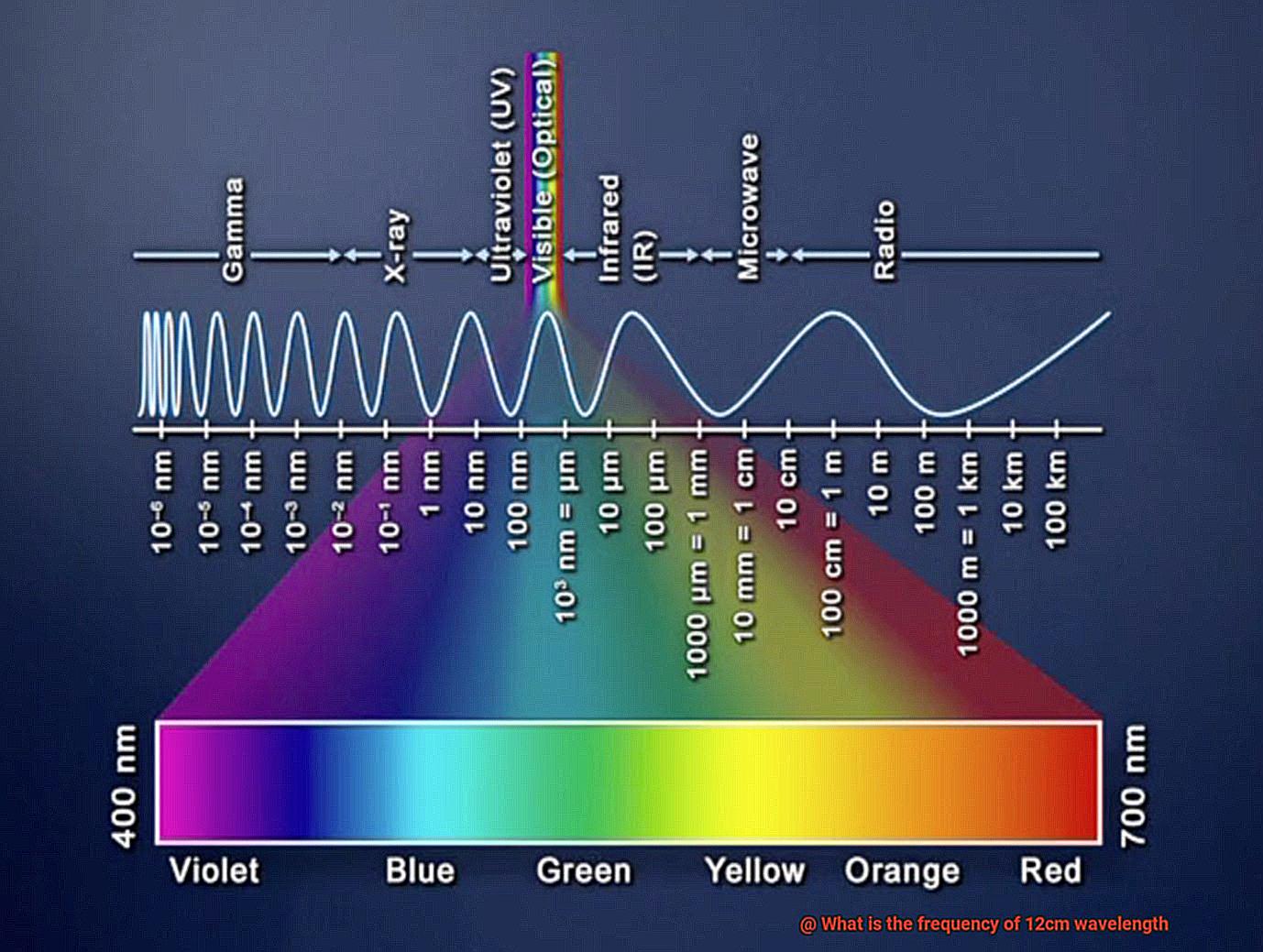
The wave equation governs the relationship between wavelength and frequency. It states that the speed of a wave is equal to its frequency multiplied by its wavelength. This means that waves with longer wavelengths have lower frequencies, while those with shorter wavelengths have higher frequencies. For example, radio waves have a longer wavelength compared to gamma rays and thus have a lower frequency.
Calculating the frequency of a wave from its wavelength is straightforward using this equation. We can use the speed of light in a vacuum, approximately 3×10^8 m/s, as a constant factor. By dividing the speed of light by the wavelength, we can determine the frequency of the wave. For instance, if we have a wave with a wavelength of 12 cm, we can find its frequency by dividing the speed of light by its wavelength: f = c/λ = (3×10^8 m/s)/(12×10^-2 m) ≈ 2.5 GHz.
The connection between wavelength and frequency has significant practical implications in various fields. In telecommunications, for instance, understanding this relationship allows engineers to design devices that can transmit signals using different frequencies and wavelengths to avoid interference. In astronomy, studying the wavelengths and frequencies of electromagnetic radiation can provide insight into celestial objects’ physical properties and composition. Similarly, spectroscopy utilizes this relationship to analyze materials’ chemical composition by examining how they absorb or emit electromagnetic radiation.
Calculating the Frequency of a Given Wavelength
This fundamental concept in physics is essential for understanding the properties and interactions of waves in various fields, from telecommunications to radio astronomy and medical imaging. So let’s dive into the math behind this relationship and explore the fascinating world of waves.
First, we need to define what wavelength and frequency are. Wavelength is the distance between two successive peaks or troughs of a wave, while frequency is the number of waves that pass through a given point in one second. In simpler terms, wavelength measures the length of a wave, while frequency measures how many waves pass by in a certain amount of time.
To calculate the frequency of a given wavelength, we use the wave equation, which states that the speed of a wave (v) is equal to its frequency (f) multiplied by its wavelength (λ): v = fλ. This equation shows us that as wavelength increases, frequency decreases, and vice versa.
So how do we apply this equation to a real-life scenario? Let’s say we have a given wavelength of 12cm (0.12m). Since we’re dealing with electromagnetic waves, we can assume that they travel at the speed of light, which is approximately 3 x 10^8 m/s. Using the wave equation and rearranging it to solve for frequency, we get: f = v/λ.
Substituting the values, we get: f = (3 x 10^8 m/s)/(0.12m) = 2.5 x 10^9 Hz. This means that the frequency of a 12cm wavelength is 2.5 x 10^9 Hz or 2.5 gigahertz (GHz), which falls within the radiofrequency range of the electromagnetic spectrum.
It’s important to note that this calculation assumes that the wave is traveling through a vacuum at the speed of light. In reality, waves can travel at different speeds depending on their medium, such as air or water. The formula used to calculate frequency may also differ slightly depending on the type of wave being analyzed.
The Speed of Light and Its Role in Calculations
The answer lies in the speed of light, a fundamental constant of physics that plays a critical role in this calculation.
The speed of light, denoted by the symbol ‘c,’ describes the speed at which electromagnetic waves, including light, travel through a vacuum. Nothing can move faster than light in a vacuum, and its value is approximately 299,792,458 meters per second or about 186,282 miles per second. It’s astonishing how fast that is.
To calculate the frequency of a wave, we need to know its wavelength and the speed at which it travels. The formula that describes this relationship is frequency = speed of light / wavelength. This means that if we know the wavelength of a wave, we can determine its frequency by dividing the speed of light by the wavelength.
For instance, suppose we have a wave with a wavelength of 12cm. In that case, we can use the formula to calculate its frequency as follows:
frequency = speed of light / wavelength
frequency = 299,792,458 m/s / 0.12 m
frequency ≈ 2.498 × 10^9 Hz
That’s pretty impressive. Therefore, the frequency of a wave with a wavelength of 12cm is approximately 2.498 × 10^9 Hz or 2.498 GHz (gigahertz).
It’s essential to note that while the speed of light is constant in a vacuum, it can change when passing through different mediums such as air, water, or glass. This change in speed is known as refraction and is responsible for various phenomena such as bending of light and mirages.
The role of the speed of light in calculating the frequency of waves is critical in fields such as telecommunications, radio astronomy, and medical imaging. It allows us to transmit information through different frequencies and wavelengths and study various phenomena in our universe.
Converting 12cm to Meters
The relationship between wavelength and frequency is crucial to understanding this concept. Wavelength is the distance between two consecutive peaks or troughs of a wave, while frequency refers to how many waves pass a given point in a second.
But what if we have a wave with a wavelength of 12cm, and we want to calculate its frequency? The first step is to convert the wavelength from centimeters to meters, since the speed of light is measured in meters per second. To do so, we simply divide 12cm by 100, which gives us 0.12 meters.
Now that we know the wavelength of the wave in meters, we can use the formula f = c / λ to calculate its frequency. The speed of light (c) is a constant value of approximately 299,792,458 meters per second (m/s), and we have the wavelength (λ) in meters. Therefore, substituting these values into the formula gives us:
f = c / λ
f = 299792458 / 0.12
f = 2,498,270,483.33 Hz
Wow. The frequency of a wave with a wavelength of 12cm is approximately 2.5 GHz (gigahertz). However, it’s important to note that this calculation assumes the wave is traveling through a vacuum. In reality, waves can travel through different mediums such as air or water, which would affect their frequency slightly.
Converting centimeters to meters is vital when calculating the frequency of a wave. Here are the key points to keep in mind:
- Wavelength is measured in distance units like centimeters or meters.
- The speed of light is measured in meters per second.
- To use the formula f = c / λ to calculate frequency, we need to know the wavelength in meters.
- Converting centimeters to meters is simple – just divide by 100.
- The frequency of a wave with a wavelength of 12cm is approximately 2.5 GHz.
Using the Formula c=λν to Calculate Frequency
Well, look no further because I’m here to guide you through the process using the formula c=λν.
First, let’s break down the formula. “C” stands for the speed of light, which is approximately 3 x 10^8 m/s. The Greek letter “λ” represents the wavelength of the wave, and “ν” represents the frequency.
Now, let’s say we have a wave with a wavelength of 12cm. To use this formula, we need to convert that measurement into meters by dividing it by 100. This gives us a wavelength of 0.12m.
Next, we can plug in our values into the formula:
c = 3 x 10^8 m/s
λ = 0.12m
3 x 10^8 = 0.12ν
Then, we can solve for the frequency (ν):
ν = (3 x 10^8) / (0.12)
ν = 2.5 x 10^9 Hz
Impressively, we can conclude that the frequency of a wave with a 12cm wavelength is approximately 2.5 x 10^9 Hz or 2.5 GHz. That means that this wave oscillates at an incredible rate of 2.5 billion cycles per second.
It’s important to note that this formula only applies to electromagnetic waves like radio waves, microwaves, and light waves. It won’t work for sound waves or other types of waves.
Moreover, this formula assumes that the wave is traveling through a vacuum or air since the speed of light varies in different materials. Therefore, it is crucial to consider your medium when using this formula.
Applying the Formula to a 12cm Wavelength
It’s a fascinating process, and we have the answers that can unravel this mystery for you. In this article, we will walk you through the simple steps on how to determine the frequency of a 12cm wavelength by applying the c=λν formula.
Firstly, let’s refresh our understanding of each variable in the formula. C represents the speed of light, λ is the wavelength, and ν is the frequency. Now that we have a clear understanding of each variable, let’s dive into the calculation.
The speed of light in a vacuum is roughly 299,792,458 meters per second (m/s). However, the wavelength given is in centimeters (cm), so we need to convert it to meters first. To do this, we can use the conversion factor that 1 cm equals 0.01 meters. Therefore, 12cm is equal to 0.12 meters.
Now, we can plug in our values into the formula:
frequency = speed of light / wavelength
frequency = 299,792,458 m/s / 0.12 m
frequency = 2,498,270,483.33 Hz
The frequency of a 12cm wavelength is approximately 2.5 GHz (gigahertz). That’s an astonishing number of cycles per second.
It’s crucial to note that frequency and wavelength are inversely proportional. This means that as the frequency increases, the wavelength decreases and vice versa. Therefore, if we were given a frequency instead of wavelength and asked to find the wavelength, we could use the same formula but rearrange it to solve for wavelength instead.
nwlhAXkzjj0″ >
Conclusion
To wrap up, electromagnetic waves are a ubiquitous presence in our daily lives, and comprehending their characteristics is vital in many domains. Wavelength denotes the distance between two adjacent crests or troughs of a wave, while frequency gauges how many waves cross through a particular point in one second. The formula c=λν, where c is the speed of light and λ is the wavelength, can be employed to determine the frequency of a 12cm wavelength.
The frequency of a 12cm wavelength is roughly 2.5 GHz (gigahertz), making it an indispensable component of our existence. From microwave ovens that utilize these waves to expedite and optimize cooking times to communication towers that depend on them for transmitting data over vast distances, comprehending this frequency can enhance our comprehension of these technologies.
Furthermore, the correlation between wavelength and frequency has significant practical implications in diverse fields such as telecommunications, radio astronomy, and medical imaging. It enables us to transmit information through various wavelengths and frequencies while also studying different phenomena throughout the universe.
In conclusion, electromagnetic waves are captivating phenomena that we encounter every day.